Im Rahmen einer Testserie an Raketentriebwerken wird eine einstufige Rakete von der Erdoberfläche aus vertikal nach oben gestartet. Die Gesamtmasse der Rakete beträgt 16,0 t. In dieser Gesamtmasse sind 13,5 t Treibstoff enthalten. Der Treibstoff verbrennt gleichmäßig und die Masse des Treibstoffs wurde so berechnet, dass die Brenndauer 75,0 s beträgt.
- Erläutern Sie das physikalische Prinzip des Raketenantriebs.
Es gilt die Beziehung Kraftstoß = Impulsänderung. Die ausströmenden Gase üben auf die Rakete einen Kraftstoß aus und erfahren dadurch eine Impulsänderung. Dabei gilt der Impulserhaltungssatz, so dass die Impulsänderung der Gase eine gleichgroße Impulsänderung der Rakete bewirkt.
Erreichbare BE-Anzahl: 2
Messungen der Beschleunigung der Rakete ergaben:
t in s 0 15,0 30,0 45,0 60,0 75,0 a in ms-2 12,19 16,07 21,62 30,19 45,19 78,19 Zeichnen Sie das a-t-Diagramm.
Begründen Sie den Verlauf des Graphen.
Parabelförmiger Verlauf läßt auf eine ungleichmäßig beschleunigte Bewegung schließen. Ursache ist die Abnahme der Gewichtskraft durch das Ausströmen der Gase bei gleichbleibender Schubkraft.
Es gilt:
für die Schubkraft gilt:
für die Gewichtskraft gilt: 
Erreichbare BE-Anzahl: 3
- Ermitteln Sie die 50,0 s nach dem Start erreichte Geschwindigkeit der Rakete (z. B.
durch grafische Integration).
Eingabe der Wertepaare in die Listenfunktion des GTR, Regression nach x4 kommt dem grafischen Verlauf am nächsten
Es ist
= 1031,632 m/s = 1,0 km/sErreichbare BE-Anzahl: 2
Berechnen Sie:
- die Masse des während des Brennvorganges pro Sekunde verbrannten Treibstoffes,
- die Schubkraft des Triebwerks zum Zeitpunkt des Starts.- Wenn in 75,0 s gerade 13,5 t Treibstoff verbrannt sind, so werden pro Sekunde 180 kg Treibstoff verbraucht.
Erreichbare BE-Anzahl: 3
Ein Kondensator der Kapazität 4,0 .10-6 F wird bis zur Spannung 150 V geladen, danach von der Spannungsquelle getrennt und zum Zeitpunkt 0 s mit einer Spule zu einem elektrischen Schwingkreis verbunden. Die Schwingung erfolgt ungedämpft. Die Spule hat die Länge 55,0 cm, die Querschnittsfläche 53,0 cm2 und 1000 Windungen. Die Permeabilitätszahl des Stoffes im Innenraum der Spule beträgt 81.
Erklären Sie, dass es nach jeder Entladung des Kondensators zu dessen erneuter Aufladung mit entgegengesetztem Vorzeichen kommt.
Erklärung über Abläufe im Schwingkreis, Selbstinduktion in der Spule bewirkt, dass der Strom gemäß LENZschem Gesetz auch nach vollständigem Entladen des Kondensators als Sebstinduktionsstrom in der ursprünglichen Richtung weiterfließt, Kondensator wird dadurch umgekehrt wieder aufgeladen, Vorgang wiederholt sich zeitlich periodisch.
Erreichbare BE-Anzahl: 3
Berechnen Sie die maximale Energie des elektrischen Feldes des Kondensators und den maximalen Wert der Stromstärke im Schwingkreis. Gehen Sie von der verlustfreien Umwandlung von elektrischer in magnetische Energie aus.
Erreichbare BE-Anzahl: 4
Berechnen Sie die Periodendauer des Schwingungsvorganges.
Skizzieren Sie den zeitlichen Verlauf von Spannung und Stromstärke für mindestens eine Periode.
Ermitteln Sie die Spannung am Kondensator für den Zeitpunkt 4,0 ms.
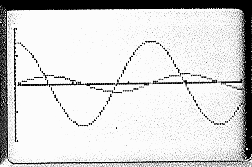
Spannungskurve als Cosinuskurve, Stromstärke als Sinuskurve, mind. 1 Periode gezeichnet
(beachten: Wenn der Schüler mit dem Rundungswert T = 0,012s weiterrechnet, ergibt sich U = -75V!)Erreichbare BE-Anzahl: 4
Erläutern Sie anhand der abgebildeten
Schaltskizze oder einer anderen geeigneten Schaltung die Erzeugung ungedämpfter
elektromagnetischer Schwingungen. Gehen Sie auch auf die Rückkopplung ein.Mittels induktiver Kopplung wird dem Schwingkreis eine Wechselspannung entnommen, deren Höhe mit dem Potentiometer eingestellt wird. Diese Spannung steuert als Basisvorspannung im Takt der Schwingung im Schwingkreis einen Transistor durch, so dass im selben Takt die Spannungsquelle Energie an den Schwingkreis abgeben kann.
Das Zurückholen eines gewissen Betrages von Energie aus dem Schwingkreis zur Steuerung der taktgerechten Energiezufuhr von einer Quelle bezeichnet man als "Rückkopplung".Erreichbare BE-Anzahl: 4