Aufgabe A: Mechanik / Elektrizitätslehre

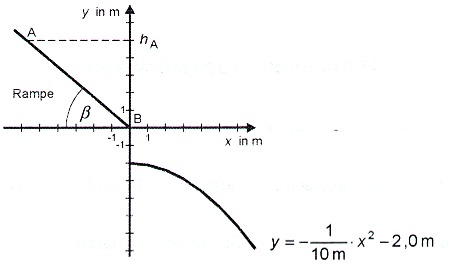
1. Ein Körper der Masse 10,0 kg gleitet entsprechend der Abbildung zunächst auf einer geneigten Rampe hinab. Er passiert die Höhe h_A = 5,0 m mit der Geschwindigkeit v_A = 1,0 m s^-1 und trifft nach dem Verlassen der Rampe auf einem parabelförmigen Hang auf. Die Reibung wird vernachlässigt.
Der Winkel ß kann verändert werden. Die Höhe h_A und die Geschwindigkeit v_A bleiben konstant.
1.1. Berechnen Sie die Abwurfgeschwindigkeit im Punkt B(0;0).

Reibung vernachlässigt heißt, Energieerhaltungssatz ist anwendbar. Folglich gilt:

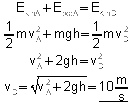
Erreichbare BE-Anzahl: 2

1.2. Ermitteln Sie die Koordinaten des Auftreffortes P₁(x_P1;y_P1) für ß = 45^o und berechnen Sie die Auftreffgeschwindigkeit des Körpers in P₁.
(Hinweis: Beachten Sie, dass der Abwurfwinkel a = -45^o beträgt.)

• Im Punkt B beginnt ein schräger Wurf mit der Gleichung
• Für den anschließenden Hang ist gegeben:
• Eingabe beider Gleichungen in den GTR,
  (Window: xMin :0, xMax: 10, yMin : -6, yMax: 2)
• Zeichnen beider Graphen, mit <GSOLV><ISCT> Schnittpunkt bestimmen.

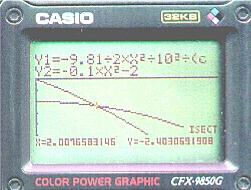
Koordinaten des Auftreffpunktes sind: x_P1 = 2,0 m; y_P1 = -2,4 m

Bestimmung von v_P:

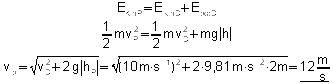
Erreichbare BE-Anzahl: 4

1.3. Der Winkel ß wird nun zwischen 30^ound 60^o variiert.
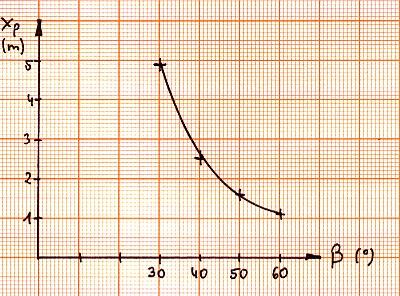
Zeichnen Sie den Graph der Funktion x_P(ß) nach Ermittlung von mindestens vier weiteren Wertepaaren.

Grafische Lösung wie in Aufgabe 1.2
In die Gleichung für die Wurfparabel werden die veränderlichen Winkel ß eingesetzt, dabei ist auf das negative Vorzeichen zu achten.

ß in o	30	0	50	60
xpin m	4,9	2,5	1,6	1,1

Erreichbare BE-Anzahl: 3

1.4. Der Gleitkörper wird durch eine Kugel ersetzt. Beim Rollen der Kugel wird keine mechanische Energie in thermische Energie umgewandelt. Vergleichen Sie die Abwurfgeschwindigkeit der Kugel qualitativ mit der des gleitenden Körpers. Begründen Sie.

Die Abwurfgeschwindigkeit einer Kugel ist im Punkt v_B kleiner als die des Gleitkörpers. Grund: Hier werden die Ausgangsenergien nicht nur in kinetische Energie der Translation umgewandelt, die den Wert v_B bestimmt. Ein Teil der Energie wird in Rotationsenergie umgewandelt, die die Translationsgeschwindigkeit herabsetzt.

Erreichbare BE-Anzahl: 2

2. Skizzieren Sie das Feldlinienbild zwischen einer negativ geladenen Platte und einer positiv geladenen Kugel (s. Abbildung).
Zwischen Platte und Kugel wird nun ein zunächst ruhender negativ geladener Probekörper freigegeben. Die Gewichtskraft des Probekörpers ist gegenüber der Feldkraft vernachlässigbar klein.
Beschreiben Sie die Bahnkurve des Probekörpers.

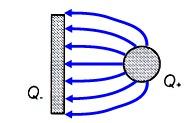
Bahnkurve des Probekörpers ist entweder eine Gerade (entlang der Symmetrieachse), im Allgemeinen aber folgt die Bahn den gekrümmten Feldlinien, die Richtung ist entgegen der Feldlinien orientiert.

Geben Sie die Bewegungsart an und begründen Sie.

Bewegungsart ist ungleichmäßig beschleunigt in Richtung Q⁺, da das Feld inhomogen ist, daraus lässt sich eine nicht konstante Feldkraft ableiten. Wegen NEWTONschem Grundgesetz F = m ^.a ist auch a nicht konstant.

Erreichbare BE-Anzahl: 5

3. Im Jahr 1909 gelang dem Amerikaner Robert A. Millikan durch die Messung der Ladung von Öltröpfchen erstmals die Bestimmung der Elementarladung.
3.1. Beschreiben Sie Aufbau, Durchführung und Auswertung dieses oder eines ähnlichen Experimentes.

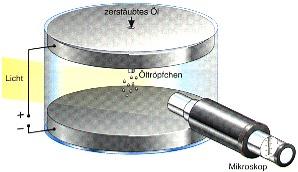An einen Plattenkondensator mit horizontalen, parallel angeordneten Platten geringen Abstandes wird eine veränderliche Gleichspannung angelegt. Mit einem Zerstäuber werden feinste Öltröpfchen in das elektrische Feld zwischen den Platten eingesprüht. Über ein Mikroskop wird die Bewegung bzw. das Schweben der Tröpfchen beobachtet und der Radius / Durchmesser des beobachteten schwebenden Tröpfchens ermittelt.
Ergebnis: Bei bestimmten Spannungswerten in diskreten Abständen stellen sich Schwebezustände einiger Tröpfchen ein, für die gilt:
Aus der Gewichtskraft des schwebenden Tröpfchens (berechnet aus Volumen, Dichte und g und der angelegten Spannung lässt sich die Ladung Q bestimmen. Die Werte lassen erkennen, dass Q stets ein ganzzahliges Vielfaches eines kleinsten Faktors ? der Elementarladung e ? ist.

Erreichbare BE-Anzahl: 5

3.2. In einem Millikankondensator mit dem Plattenabstand 5,0 mm wird ein schwebendes Öltröpfchen mit dem Radius 9,0 ^.10^-4 mm beobachtet. Die Dichte des Öls beträgt 0,90g^. cm ^-3.
Berechnen Sie die am Kondensator anliegende Spannung für den Fall, dass die Ladung des Öltröpfchens 5^. e beträgt.

Für den Schwebezustand eines Öltropfens gilt das Kräftegleichgewicht

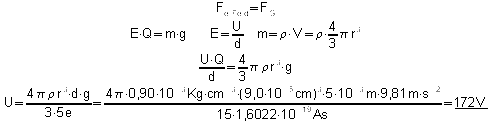
Erreichbare BE-Anzahl: 4