Wählen Sie eine der nachstehenden Aufgaben aus und bearbeiten Sie diese.

Aufgabe C1: Mechanik

Untersuchen Sie die Energieumwandlungen, die beim zentralen geraden Stoß zwischen den Körpern von zwei bifilar aufgehängten Fadenpendeln stattfinden. Der Stoß erfolgt weitgehend unelastisch (ein geringes Abprallen während des Stoßvorganges ist unerheblich, die Pendelkörper sollten sich jedoch kurz nach dem Stoß mit gemeinsamer Geschwindigkeit bewegen). Die Experimentieranordnung wird Ihnen vollständig aufgebaut übergeben.
1. Bestimmen Sie die Massen der Pendelkörper und die Länge der Fadenpendel.

Massenbestimmung, z.B. m₁ = 20g, 50g, 100g, 150g, m₂ = 140g

Erreichbare BE-Anzahl: 1

2. Lenken Sie den rechten Pendelkörper 15 cm in horizontaler Richtung nach rechts aus und geben Sie ihn frei. Messen Sie die Amplitude der Schwingung beider Pendelkörper nach dem Stoß. Wiederholen Sie das Experiment mehrmals und bilden Sie den Mittelwert der gemessenen Amplituden. Ersetzen Sie den rechten Pendelkörper nacheinander durch die zwei Pendelkörper anderer Masse und bestimmen Sie erneut jeweils den Mittelwert der Amplituden.
(Hinweis: Damit der Stoß möglichst zentral erfolgt, kann ein Nachkorrigieren der Pendellänge des stoßenden Körpers erforderlich sein.)

Messwerte für die Amplituden (bei der eigenen Experimentieranordnung gemessen):

	Auslenkung y in cm				Mittelwert
m1 = 50g	4,5	5,0	4,8	5,0	4,8
m2 = 100g	7,0	7,2	7,0	6,9	7,0
m3 = 150g	9,0	8,0	8,0	8,1	8,3

Erreichbare BE-Anzahl: 4

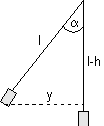
3. Berechnen Sie die Geschwindigkeit, die der rechte Pendelkörper unmittelbar vor dem Stoß besaß.

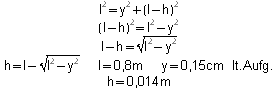
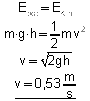
Erreichbare BE-Anzahl: 2

4. Berechnen Sie jeweils aus den Mittelwerten der unter 2 gemessenen Amplituden die Geschwindigkeit, die beide Pendelkörper unmittelbar nach dem Stoß besaßen sowie den Prozentsatz p % an mechanischer Energie, der während des Stoßvorganges in thermische Energie umgewandelt wurde.
Führen Sie eine Fehlerbetrachtung durch (Beurteilen der Genauigkeit der Messwerte sowie der Ergebnisse).
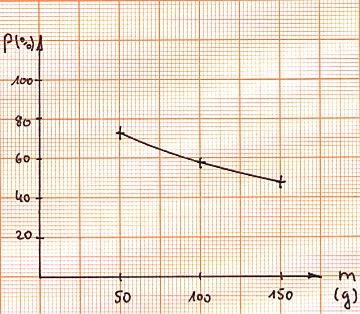
Stellen Sie den Prozentsatz in Abhängigkeit von der Masse des rechten Pendelkörpers grafisch dar.

	u in m s-1	EKinA in 10-3Nm	EKinE in 10-3Nm	p(%)
m1 = 50g	0,14	7,02	1,85	73,7
m2 = 100g	0,22	14,0	5,85	58,3
m3 = 150g	0,27	21,0	10,9	48,3

Fehlerbetrachtung: (Sinnvolle zufällige und systematische Fehler)

Erreichbare BE-Anzahl: 6

5. Ein Körper der Masse m₁ stößt mit der Geschwindigkeit v₁ einen zweiten ruhenden Körper der Masse m₂ zentral, gerade und vollkommen unelastisch. Zeigen Sie, dass für den Zusammenhang zwischen dem Prozentsatz p % der mechanischen Energie, die beim Stoß in thermische Energie umgewandelt wird, und der Masse m₁ gilt:

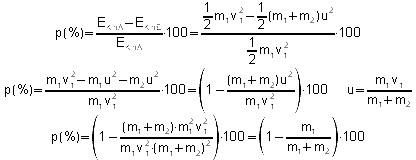
Erreichbare BE-Anzahl: 2

Aufgabe C2: Optik

Bestimmen Sie die Gitterkonstante eines optischen Gitters.
Planen Sie die Experimente gemäß der folgenden Aufgabenstellungen und fordern Sie bei Ihrem Lehrer die erforderlichen Geräte und Hilfsmittel an.

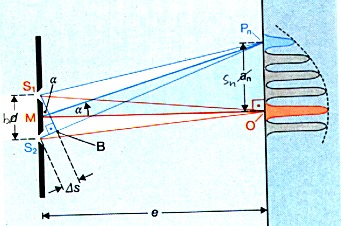
1. Erläutern Sie die Entstehung der Interferenzstreifen 1. Ordnung an einem Doppelspalt.
Leiten Sie eine Gleichung her, mit der aus dem Abstand zwischen dem Interferenzstreifen 0. Ordnung und einem Interferenzstreifen 1. Ordnung der Spaltabstand des Doppelspalts berechnet werden kann.

Voraussetzung für die Entstehung eines Interferenzmusters ist zunächst kohärentes Licht, welches aus einem LASER kommt oder durch eine konventionelle Lichtquelle mit einer geringen Spaltblende annähernd hergestellt wird.
Beim Durchgang durch die Öffnungen des Gitters erfolgt eine Beugung der Teilwellen kohärenten Lichtes. Durch diese Richtungsänderung kommt es zur ungestörten Überlagerung der Wellen und an bestimmten Stellen zu Interferenz. Bei einem Gangunterschied von erfolgt Schwächung bis zur Auslöschung, bei einem Gangunterschied von erfolgt eine Verstärkung des Lichtes. Dort sind auf einem Schirm dann helle Interferenzstreifen 1.Ordnung sichtbar.
Herleitung:

• Zum mittleren, hellen Streifen - dem Interferenzmaximum 0. Ordnung - haben beide Elementarwellen den gleichen Weg zurückzulegen. Sie sind demzufolge amplituden- und phasengleich, so dass ihr Gangunterschied ist.
• Für die Maxima 1. ist der Gangunterschied Somit kommt es an diesen Orten zur Verstärkung und damit zum hellen Interferenzstreifen.
• Da der Abstand e (Gitter - Schirm) wesentlich größer ist als der Spaltabstand b, können die beiden Wellenzüge als nahezu parallel betrachtet werden. Ihre gemeinsame Richtung ist dann MP_n.
• Trägt man den Abstand P_nS₁ auf P_nS₂ ab, so gibt die Reststrecke BS₂ den Gangunterschied Ds an.
• Die Dreiecke MOP_n und S₁S₂B sind mit o.g. Vereinfachung näherungsweise ähnlich.
  Für den Richtungswinkel a der Wellenzüge gilt dann:
• Wegen gilt für kleine Winkel Damit lassen sich die Gleichungen (1) und (2) zusammenfassen zu:
  

Erreichbare BE-Anzahl: 5

2. Bestimmen Sie mit zwei vorgegebenen experimentellen Methoden die Gitterkonstante b des gegebenen optischen Gitters.

2.1. Methode l:
Auf einem Schirm sollen mit Hilfe des gegebenen Gitters lnterferenzstreifen abgebildet werden. Fertigen Sie eine Skizze des Versuchsaufbaus an. Bauen Sie die Versuchsanordnung auf, bilden Sie die lnterferenzstreifen ab und messen Sie die erforderlichen Größen.
Die mittlere Wellenlänge des vom verwendeten Farbfilter durchgelassenen Lichtanteils wird Ihnen vom Lehrer mitgeteilt.
Berechnen Sie die Gitterkonstante b.

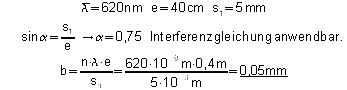
Erreichbare BE-Anzahl: 7

2.2. Methode 2:
Stellen Sie unmittelbar vor eine Experimentierleuchte (ohne Leuchtspalt) den bei 2.1 verwendeten Farbfilter sowie die gegebene Blende mit zwei kleinen kreisförmigen Öffnungen. Betrachten Sie die Blende aus einer Entfernung von etwa 30 cm durch das optische Gitter, das Sie dicht vor ein Auge halten. Stellen Sie nun den Abstand zwischen Gitter und Blende so ein, dass das rechte Maximum 1. Ordnung der linken Öffnung unter oder über dem linken Maximum 1. Ordnung der rechten Öffnung liegt.
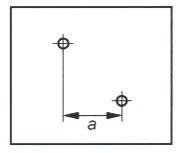
Messen Sie den Abstand e zwischen Gitter und Blende sowie den horizontalen Abstand a zwischen den Öffnungen der Blende (Siehe Abbildung).
Mit der Gleichung kann die Gitterkonstante b näherungsweise berechnet werden. Berechnen Sie b.

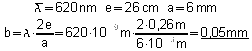
Erreichbare BE-Anzahl: 3