
Schriftliche Abschlussprüfung Physik 2000/2001
Aufgabe 5 Mechanische Schwingungen
5.1 Schülerexperiment
Wählen Sie nur eines der Schülerexperimente 5.1.1 Fadenpendel oder 5.1.2 Federschwinger aus.
5.1.1 Fadenpendel
Aufgabe: Untersuchen Sie die Veränderung der Periodendauer T und der Frequenz f eines Fadenpendels bei Vervierfachung seiner Pendellänge l.
Vorbereitung:
- Skizzieren Sie den Aufbau Ihres Experimentes.
- Entwerfen Sie eine Messwerttabelle für die Pendellängen 20 cm und 80 cm.
Durchführung:
- Bauen Sie die Experimentieranordnung nach Ihrer Skizze auf.
- Messen Sie jeweils die Zeit für 10 Schwingungen (bei kleinen Amplituden).
- Bestimmen Sie daraus für beide Pendellängen Periodendauer und Frequenz.
- Notieren Sie die Werte in der Tabelle.
Auswertung:
- Ermitteln Sie mithilfe Ihrer Messwerte den Faktor, um den sich die Periodendauer bei Vervierfachung der Pendellänge geändert hat.
- Untersuchen Sie diesen Zusammenhang durch Berechnung der Periodendauer für die gegebenen Pendellängen.
- Nennen Sie einen Grund für die möglicherweise auftretende Abweichung zwischen berechnetem und experimentell rmitteltem Wert.
- Geben Sie die Veränderung der Frequenz bei Vervierfachung der Pendellänge an.
Für 5. 1.1 erreichbare BE: 12
Setzen Sie mit Teilaufgabe 5.2 fort.
5.1.2 Federschwinger
Aufgabe: Untersuchen Sie die Veränderung der Periodendauer T und der Frequenz f eines Federschwingers bei Vervierfachung seiner Masse m.
Vorbereitung:
- Skizzieren Sie den Aufbau Ihres Experimentes.
- Entwerfen Sie eine Messwerttabelle für die Massen 30 g und 120 g.
Durchführung:
- Bauen Sie die Experimentieranordnung nach Ihrer Skizze auf.
- Messen Sie jeweils die Zeit für 10 Schwingungen (bei kleinen Amplituden).
- Bestimmen Sie daraus für beide Massen Periodendauer und Frequenz.
- Notieren Sie die Werte in der Tabelle.
Auswertung:
- Ermitteln Sie mit Hilfe Ihrer Messwerte den Faktor, um den sich die Periodendauer bei Vervierfachung der Masse geändert hat.
- Untersuchen Sie diesen Zusammenhang durch Berechnung der Periodendauer für die gegebenen Massen. Die Federkonstante wird Ihnen vom Aufsicht führenden Lehrer mitgeteilt.
- Nennen Sie einen Grund für die möglicherweise auftretende Abweichung zwischen berechnetem und experimentell ermitteltem Wert.
- Geben Sie die Veränderung der Frequenz bei Vervierfachung der Masse an.
Für 5.1.2 erreichbare BE: 12
5.2
Eine Kugel wird am Rande einer gewölbten Bahn losgelassen. In der Zeit
12 s führt die Kugel 10 Hin- und Herbewegungen aus, bevor sie im tiefsten Punkt der Bahn
zur Ruhe kommt.

5.2.1 Entscheiden Sie, ob es sich dabei um eine ungedämpfte oder um eine gedämpfte Schwingung handelt. Begründen Sie Ihre Entscheidung.
5.2.2 Ermitteln Sie Periodendauer und Frequenz dieser Schwingung.
5.2.3 Erläutern Sie, was man unter der Frequenz einer Schwingung versteht.
5.2.4 Skizzieren Sie ein y-t-Diagramm des in 5.2 beschriebenen Vorganges für wenigstens zwei Perioden.
5.2.5 Nennen Sie die dabei auftretenden Energieumwandlungen.
Für 5.2.1 bis 5.2.5 erreichbare BE: 13
Lösung
Aufgabe 5 Mechanische Schwingungen
(Bitte
beachten Sie den Hinweis am Ende der Seite)
Aufgabe 5.1.1
Skizze:
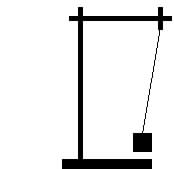
Messwerttabelle:
Messwerte |
Berechnete Werte |
||
l in cm |
t in s |
T in s |
f in Hz |
20 |
9,35 |
0,935 |
1,07 |
80 |
18,19 |
1,819 |
0,550 |
(Entsprechend der Aufgabenstellung wird T mit Hilfe der Gleichung T = t : 10 und f mit f = 1 : T berechnet)
Auswertung:
1,819 s : 0,935 s » 2
Bei der Vervierfachung der Pendellänge verdoppelt sich die Schwingungsdauer.
Ges.: T
geg.: I: l = 20 cm = 0,2 m
II: l = 80 cm = 0,8 m
Lösung I:
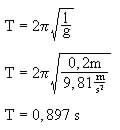
Lösung II:
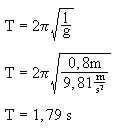
Zusammenhang: 1,79 s : 0,897 s » 2
Grund für Abweichungen: Ungenaues
Einstellen der Pendellänge
(Auch möglich: Verwendung eines zu leichten Massestückes, Fehler beim Messen der
Zeit, zu weites Auslenken des Pendels - "Schlingerbewegungen" oder Anstoßen des
Pendels)
Bei Vervierfachung der Pendellänge
halbiert sich die Frequenz.
(Begründung: Da sich die Schwingungsdauer verdoppelt und T = 1 : f gilt, halbiert
sich die Frequenz)
Aufgabe 5.1.2
Skizze:
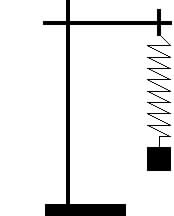
Messwerte:
Messwerte |
Berechnete Werte |
||
m in g |
t in s |
T in s |
f in Hz |
30 |
4,89 |
0,489 |
2,04 |
120 |
9,75 |
0,975 |
1,03 |
(Entsprechend der Aufgabenstellung wird T mit Hilfe der Gleichung T = t : 10 und f mit f = 1 : T berechnet)
Auswertung:
0,975 s : 0,489 s =1,994 » 2.
Bei der Vervierfachung der Masse hat sich die Schwingungsdauer verdoppelt.
Ges.: T
geg.: I: m = 30 g = 0,03 kg; k = 5,0 ![]()
II: m = 120 g = 0,12 kg: k = 5,0 ![]()
Lösung I:

Lösung II:

Zusammenhang: 0,973 s : 0,487 s = 1,999 » 2
Grund für Abweichung: Ungenauigkeiten
beim Messen der Zeit
(Weitere Gründe: Zu starke Auslenkung der Feder, Verwendung
falscher Massenstücke)
Bei Vervierfachung der Pendellänge
halbiert sich die Frequenz.
(Begründung: Da sich die Schwingungsdauer verdoppelt und T = 1 : f gilt,
halbiert sich die Frequenz)
Aufgabe 5.2
5.2.1 Es handelt sich um eine gedämpfte Schwingung, da die Bewegung zum Stillstand kommt.
5.2.2. Ges.: T, f
geg.: t = 12 s, n = 10
Lösung:
1. Berechnung der Schwingungsdauer:
T = t : n
T = 12 s : 10
T = 1,2 s
2. Berechung der Frequenz:
f = 1 : T
f = 1 : 1,2 s
f = 0,83 Hz
Die Schwingungsdauer beträgt 1,2 s, die Frequenz 0,83 Hz.
5.2.3 Die Frequenz einer Schwingung gibt die Anzahl der vollständigen Schwingungen pro Sekunde an.
5.2.4
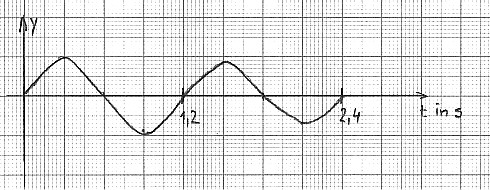
(Akzeptabel wäre aus Sicht der Autoren auch das
Diagramm einer ungedämpften Schwingung, da während der ersten beiden Schwingungen der
Unterschied in der Amplitude noch nicht so signifikant ist und keine Angabe der Amplitude
in der Aufgabenstellung erfolgte.)
5.2.5 Epot
« Ekin
Ekin ® Etherm
Die vorliegenden Lösungen sind Musterlösungen von Henri Schönbach, 83. Mittelschule, und , Georg-Schumann-Schule in Leipzig, und keine offiziellen Lösungen des Sächsischen Staatsministeriums für Kultus.Herzlicher Dank gilt Herrn Dr. Liebau und Frau Ines Stiller, die die vorliegenden Lösungen begutachteten. Die Autoren garantieren nicht für die Vollständigkeit und Richtigkeit der vorliegenden Lösungen. In Klammern stehende und kleiner gedruckte Lösungen betrachten die Autoren auch als möglich bzw. sind als Kommentar gedacht. Wir freuen uns über jeden Hinweis zur Verbesserung dieser Musterlösungen. Bitte senden Sie uns eine Email, Betreff: Prüfung 2001