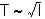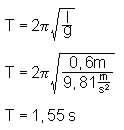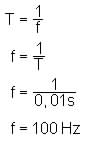5.1 Schülerexperiment: Fadenpendel
oder Federschwinger
Wählen Sie nur eines der Schülerexperimente!
Aufgabe:
Untersuchen Sie die Abhängigkeit der Periodendauer T eines Fadenpendels
von seiner Länge l!
Vorbereitung:
1. Skizzieren Sie den Versuchsaufbau!
2. Entwerfen Sie eine Messwerttabelle für die Pendellängen 0, 15
m; 0,3 m; 0,45 m und 0,6 m!
Durchführung:
1. Bauen Sie die Experimentieranordnung nach Ihrer Skizze auf!
2. Messen Sie jeweils die Zeit für 10 Schwingungen und bestimmen Sie
daraus die Periodendauer!
3. Notieren Sie die Werte in der Tabelle!
Auswertung:
1. Zeichnen Sie entsprechend Ihrer Messwertreihe ein T-l-Diagramm!
2. Welcher Zusammenhang besteht zwischen der Periodendauer und der Pendellänge?
3. Berechnen Sie die Periodendauer für die Pendellänge 0,6 m!
4. Vergleichen Sie den berechneten Wert mit dem gemessenen Wert der Periodendauer!
5.Geben Sie eine mögliche Fehlerquelle beim Experimentieren an!
Aufgabe:
Untersuchen Sie die Abhängigkeit der Periodendauer T eines Federschwingers
von der Masse m!
Vorbereitung:
1. Skizzieren Sie den Versuchsaufbau!
2. Entwerfen Sie eine Messwerttabelle für die Massen 40g; 60g; 80g und
100g!
Durchführung:
1. Bauen Sie die Experimentieranordnung nach Ihrer Skizze auf!
2. Messen Sie jeweils die Zeit für 10 Schwingungen und bestimmen Sie
daraus die Periodendauer!
3. Notieren Sie die Werte in der Tabelle!
Auswertung:
1. Zeichnen Sie entsprechend Ihrer Messwertreihe ein T-m-Diagramm!
2. Welcher Zusammenhang besteht zwischen der Periodendauer und der Masse?
3. Berechnen Sie die Periodendauer für die Masse 100g! (Den Wert der
Federkonstante teilt Ihnen der Physiklehrer mit.)
4. Vergleichen Sie den berechneten Wert mit dem gemessenen Wert der Periodendauer!
5. Geben Sie eine mögliche Fehlerquelle beim Experimentieren an!
5.2 Eine Schwingung hat eine Periodendauer von 0,01
s bei gleichbleibender Amplitude von 1,5cm.
5.2.1 Zeichnen Sie das zugehörige y - t - Diagramm für zwei
Perioden!
5.2.2 Berechnen Sie die Frequenz der Schwingung!
5.3 Mechanische Wellen
5.3.1 Erläutern Sie an einem selbstgewählten Beispiel die
folgenden Merkmale mechanischer Wellen: Ausbreitungsgeschwindigkeit, Frequenz,
und Wellenlänge!
5.3.2 Begründen Sie die Notwendigkeit des Lärmschutzes!Beschreiben
Sie mögliche Maßnahmen an einem Beispiel!
Aufgabe 5.1 Schülerexperiment Fadenpendel
Vorbereitung / Durchführung:
Versuchsaufbau:
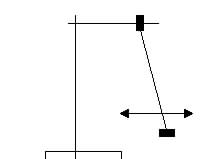
Messwerttabelle:

Auswertung:
1.
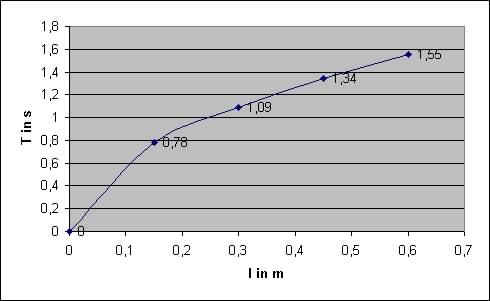
2. 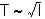
3.
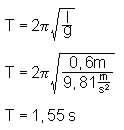
4. Tber. »
Tgem
5. Ungenaues Einstellen der Fadenlänge, ungenaue Zeitmessungen
Aufgabe 5.2
5.2.1
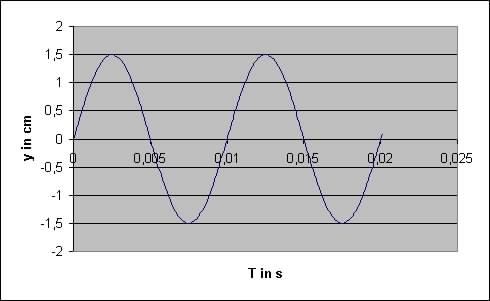
5.2.2 ges.: f
geg.: T = 0,01 s
Lösung:
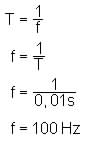
Die Frequenz der Schwingung beträgt 100 Hz.
Aufgabe 5.3
5.3.1 Beispiel: Wasserwellen
Die Ausbreitungsgeschwindigkeit gibt an, wie schnell
sich eine Schwingung im Raum ausbreitet. Man beobachtet also die Ausbreitung
einer einzelnen Schwingung im Wasser, misst Entfernung und für die
Ausbreitung benötigte Zeit und kann so die Ausbreitungsgeschwindigkeit
berechnen.
Die Frequenz gibt an, wie viele Schwingungen in einer
Sekunde ausgeführt werden. Dazu muss man bei Wasserwellen die Anzahl
der Wellenberge oder -täler in einer bestimmten Zeit (z. B. 10s) zählen
und dann ausrechnen, wie viele dieser Schwingungen pro Sekunde stattfinden.
Die Wellenlänge ist die Entfernung zwischen zwei
benachbarten Körpern oder Teilchen im gleichen Schwingungszustand.
Bei Wasserwellen könnte man die Wellenlänge also durch Messen
des Abstandes zwischen zwei Wellenbergen bestimmen.
5.3.2 Man muss sich
vor Lärm schützen, um gesundheitliche Schäden (z. B. Schwerhörigkeit)
zu vermeiden.
Eine Möglichkeit des Lärmschutzes zu Hause besteht
in der Verwendung sogenannter "Lärmschutzfenster". Diese bestehen aus
zwei dicken Glasscheiben (unterschiedliche Dicke) und einem breiten Zwischenraum,
so dass der Lärm in möglichst vielen Frequenzbereichen gedämpft
werden kann.