| STARTSEITE | BINSUM | LAGEPGE | EBENE | TANG-NOR | Downloads |
Beschreibung
Das Programm hilft bei der Wahrscheinlichkeitsberechnung P(k) eines n-stufigen Bernoulli-Versuches. Es wird bei diesem Programm nur die Einzelwahrscheinlichkeit ausgerechnet. Es handelt sich um eine Binomialverteilung, wenn die Wahrscheinlichkeit der betrachteten Elemente nach jeder Ziehung gleich bleibt (es wird 'zurückgelegt').
Mit anderen Worten:
B(n;p)
gesucht: P(k)
Folgendes muss eingegeben werden:
GES ANZ? n = Gesamtanzahl der Versuche
EINZ WKT? p = Wahrscheinlichkeit des betrachteten Elements
ANZAHL? k = wie oft das betrachtete Element vorkommen soll
Die Bestätigung erfolgt jeweils mit EXE. Nach erfolgter Eingabe wird die Wahrscheinlichkeit angezeigt:
WKT =... angezeigte Wahrscheinlichkeit ist P(k)
Achtung!
Falls n · p ( 1 - p ) > 9 ist, wird die Näherungsformel von Moivre-Laplace verwendet, da der Taschenrechner die Berechnung nicht mehr schafft.
Beispielaufgabe
(ähnlich Abituraufgabe Grundkurs Mathematik Sachsen 2007, Teil C Stochastik)
Bei einem Gewinnspiel werden aus einer Urne bedruckte Kronkorken gezogen. Folgende Kronkorken sind enthalten:
100 Kronkorken, davon
20 mit dem Buchstaben A
15 mit dem Buchstaben B
40 mit dem Buchstaben C
25 mit anderen Buchstaben
Bei dem Spiel werden drei Kronkorken entnommen und wieder zurückgelegt.
Wie hoch ist die Wahrscheinlichkeit folgender Ereignisse:
Ereignis A: Mindestens zwei Kronkorken tragen den Buchstaben A.
Ereignis B: Es wird genau zweimal der Buchstabe B gezogen.
Berechnung Ereignis A:
Nur mit BINSUM möglich, da k einen Bereich (2 oder 3 Kronkorken) umfasst.
Berechnung Ereignis B:
Die Berechnung geht auch mit BINSUM.
1. Programm BINOMIAL starten.
2. Eingabe der Daten und Bestätigung mit EXE.
| erste
Eingabe: GES ANZ? n = 3 (da 3 Kronkorken insgesamt gezogen werden) |
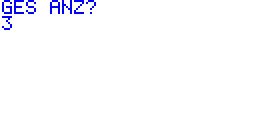 |
| zweite Eingabe: EINZ WKT? p = 0,15 (da 15 von 100 Kronkorken mit dem Buchstaben B versehen sind) |
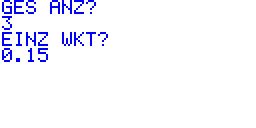 |
| dritte
Eingabe: ANZAHL? k = 2 (da B genau zweimal gezogen werden soll) |
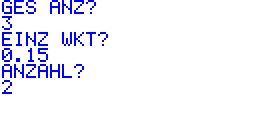 |
| nun
erfolgt die Berechnung: WKT = 0,057375 (die berechnete Einzelwahrscheinlichkeit) |
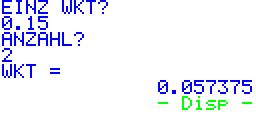 |
Mathematische Schreibweise:
B(3;0,15)
P(k=2) ≈ 5,74 %
Antwortsatz:
Die Wahrscheinlichkeit, dass genau 2 Kronkorken mit dem Buchstaben B gezogen werden, beträgt rund 5,74 %.