| BINOMIAL | BINSUM | LAGEPGE | EBENE | STARTSEITE | Downloads |
Beschreibung
Das Programm zeigt euch die Funktionsgleichung der Tangente und der Normale in einem beliebigen Punkt einer Funktion an. Die Funktion muss vorher im Graph-Menü als Y1 eingegeben werden. Nach dem Starten des Programmes wird man aufgefordert, den x-Wert des Punktes einzugeben, in dem die Tangente und Normale angelegt werden soll. Es werden der Berührungspunkt P(x; y) und die Funktion der Tangente und Normale angezeigt. Die Bestätigung erfolgt jeweils mit EXE.
Beispielaufgabe
(ähnlich Abituraufgabe Grundkurs Mathematik Sachsen 2007, Teil A Analysis)
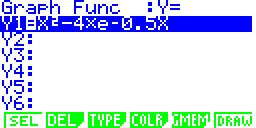
Die Funktion f(x) ist durch die Gleichung y = f(x) = x2 - 4 ⋅ e-0,5x ( x ∈ D ) gegeben.
a) Ermitteln Sie die Gleichung der Tangente t an den Graphen der Funktion f(x) an der Stelle
x = 0,5.
b) Ermitteln Sie die Fläche, die von der Gerade t und den Koordinatenachsen begrenzt wird.
Berechnung a)
|
Die Funktiongleichung y = f(x) = x2 - 4 ⋅ e−0,5x im Graph-Menü als Y1 eingeben. |
 |
| Zunächst den Kurvenverlauf betrachten, um eine Vorstellung der Funktion zu verschaffen. | 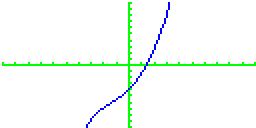 |
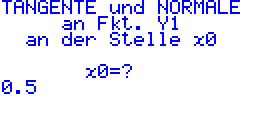
| Als nächstes das Programm TANG-NOR starten, den Punkt x = 0,5 eingeben und mit EXE bestätigen. |
 |
|
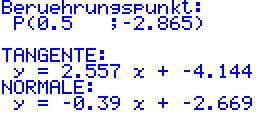
Der Berührungspunkt sowie die Gleichnungen der Tangente und Normale werden vom Programm angezeigt. Tangentenfunktion: y = 2,557x - 4,144 |
 |
| Zur Kontrolle die Tangentenfunktion y = 2,557x - 4,144 in das Graph-Menü eingeben... |
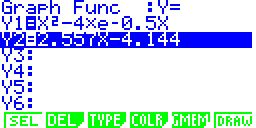 |
| ...und prüfen, ob die Tangente an der richtigen Stelle liegt. Ich denke, das passt :). | 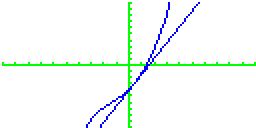 |
Lösung zu a)
Die Geradengleichung von t lautet y = 2,557x - 4,144.
Berechnung b)
Die Berechnung der Fläche wird im Graph-Menü vorgenommen, ohne das Programm TANG-NOR.
| Wenn die Kurven beider Funktionen zu sehen sind, SHIFT-F5 drücken. Danach F6 drücken, damit das Integral-Symbol erscheint. Dieses wird mit F3 bestätigt. | 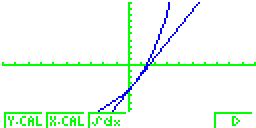 |
| Nun mit der RUNTER-Taste die Tangentengleichung y = 2,557x - 4,144 auswählen und mit EXE bestätigen. |
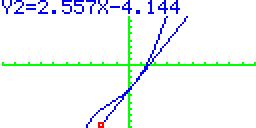 |
| Da die Fläche durch die Koordinatenachsen bestimmt wird, wird als Startpunkt x = 0 festgelegt und mit EXE bestätigt. | 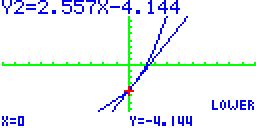 |
| Als Endpunkt wird y = 0 (näherungsweise) festgelegt und mit EXE bestätigt. | 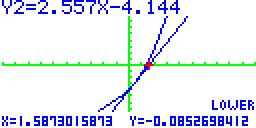 |
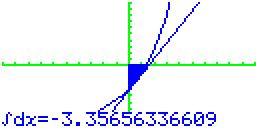
| Der
Betrag des angezeigten Wertes des Integrals ist der Inhalt der
Fläche A, die durch die Gerade t und die Koordinatenachsen
begrenzt wird. A ≈ 3,357 FE |
 |
Lösung zu b)
Der Flächeninhalt A zwischen der Geraden t und den Koordinatenachsen beträgt rund
3,357 Flächeneinheiten.