| BINOMIAL | BINSUM | STARTSEITE | EBENE | TANG-NOR | Downloads |
Beschreibung (oder zur Beispielaufgabe)
ACHTUNG - einige Lagebeziehungsunterprogramme aus den Programmsammlungen Mathe200x sind fehlerhaft!
Dies trifft wohl auch auf Mathe2000 zu!
Bitte prüfen Sie mit den Geraden (2|1|0)+s(1|-1|0) und (5|9|0)+t(2|9|0)
-> Schnittpunkt müsste (3|0|0) sein!
Fehlerfrei dürfte MATHE2005 sein.
Mit dem Programm LAGEPGE lassen sich Lagebeziehungen im Koordinatensystem anzeigen. Als erstes muss ausgewählt werden, zwischen welchen Elementen der Vektorrechnung die Lagebeziehung ermittelt werden soll. Folgende Optionen sind möglich:
| 1
E - P (Ebene - Punkt) 2 E - g (Ebene - Gerade) 3 E - E (Ebene - Ebene) |
4
g - P (Gerade - Punkt) 5 g - g (Gerade - Gerade) 6 P - P (Punkt - Punkt) |
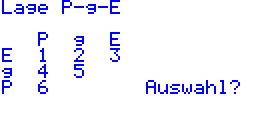 |
Die Bestätigung der Eingabe erfolgt jeweils mit der EXE-Taste.
1. Lagebeziehung zwischen Ebene & Punkt
Die Eingabe des Punktes erfolgt über die x - y - z Koordinaten. Die Ebene muss in allgemeiner Form eingegeben werden (a, b, c, d). Liegt der Punkt außerhalb der Ebene, so wird der Abstand angezeigt.
2. Lagebeziehung zwischen Ebene & Gerade
Die Eingabe der Geraden erfolgt über den Aufpunkt (x, y, z) und den Richtungsvektor (ax, ay, az). Die Ebene muss in allgemeiner Form eingegeben werden (a, b, c, d). Es wird angezeigt, ob die Gerade in der Ebene liegt, parallel dazu ist oder sie schneidet. Ist sie parallel, wird der Abstand angezeigt. Schneidet die Gerade die Ebene, so wird der Schnittpunkt und der Schnittwinkel zwischen Ebene und Gerade angezeigt.
3. Lagebeziehung zwischen Ebene & Ebene
Die Ebenen müssen in allgemeiner Form eingegeben werden (a, b, c, d). Es wird angezeigt, ob die Ebenen identisch sind, getrennt parallel sind, oder ob sie sich schneiden. Sind sie getrennt parallel, wird der Abstand angezeigt. Schneiden die Ebenen sich, so werden die Schnittgerade und der Schnittwinkel zwischen den beiden Ebenen angezeigt.
4. Lagebeziehung zwischen Gerade & Punkt
Die Eingabe des Punktes erfolgt über die x - y - z Koordinaten. Die Eingabe der Geraden erfolgt über den Aufpunktvektor (x, y, z) und den Richtungsvektor (ax, ay, az). Es wird angezeigt, ob der Punkt auf der Ebene liegt oder welchen Abstand er zur Geraden hat.
5. Lagebeziehung zwischen Gerade & Gerade
Die Eingabe der beiden Geraden erfolgt über den Aufpunktvektor (x, y, z) und den Richtungsvektor (ax, ay, az). Es wird angezeigt, ob die Geraden windschief (mit kürzestem Abstand), getrennt parallel zu zueinander (mit Abstand) oder identisch sind.
6. Lagebeziehung zwischen Punkt & Punkt
Die Eingabe der beiden Punkte erfolgt über die x - y - z Koordinaten. Sind die Punkte nicht identisch, so wird deren Abstand sowie deren Verbindungsgerade angezeigt.
Beispielaufgabe
(ähnlich der Grundkurs Abituraufgabe Sachsen 2007, Teil B Geometrie)
In einem kartesischen Koordinatensystem sind folgende Punkte gegeben:
| A(-2; -1; -2) | B(4; -3; -2) | C(0; 5; -2) | S(2; 1; 5,5) |
Diese Punkte sind Eckpunkte einer dreiseitigen Pyramide mit der Spitze S.
Berechnen Sie die Höhe und das Volumen dieser Pyramide.
Lösung
Um die Höhe auszurechnen, wird die Ebene, auf der sich die Grundfläche der Pyramide (ABC) befindet, mit dem Programm EBENE parameterfrei gemacht. (siehe Beispiel EBENE)
| Das Programm LAGEPGE starten, die Lagebeziehung zwischen Punkt und Ebene mit der Taste 1 auswählen und mit EXE bestätigen. | 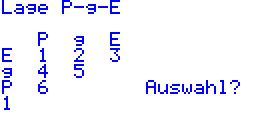 |
| Als nächstes werden die Koordinaten von Punkt S eingegeben und mit EXE bestätigt... |  |
| ... und danach die Ebenengleichung in parameterfreier Form. |  |
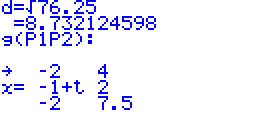
| Wenn
die
Koordinaten erfolgreich eingegeben wurden, wird die Lagebeziehung
angezeigt. Der Punkt liegt außerhalb der Ebene und hat einen
Abstand von 7,5 Längeneinheiten. hP = 7,5 LE |
 |
Antwortsatz:
Die Höhe der Pyramide beträgt 7,5 Längeneinheiten.
Das Volumen der Pyramide lässt sich über das Spatvolumen des Tetraeders berechnen.
| Formel: | 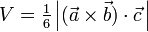 |
Dazu müssen als erstes die Richtungsvektoren
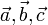 mit LAGEPGE ausgerechnet werden.
mit LAGEPGE ausgerechnet werden.| Lagebeziehung zwischen Punkt und Punkt mit Taste 6 auswählen und bestätigen. |  |
||
| Vektor zum Punkt A als Aufpunktvektor eingeben. |  |
||
| Den dazugehörigen Ortsvektor nach B eingeben. |  |
||
|
 |
||
| Programm wiederholen, Lagebeziehung zwischen Punkt und Punkt mit Taste 6 auswählen und bestätigen. |  |
||
| Ortsvektor nach A als Aufpunktvektor eingeben. |  |
||
| Den dazugehörigen Ortsvektor nach C eingeben. |  |
||
|
 |
||
| Programm wiederholen, Lagebeziehung zwischen Punkt und Punkt mit Taste 6 auswählen und bestätigen. |  |
||
| Ortsvektor nach A als Aufpunktvektor eingeben. |  |
||
| Den dazugehörigen Ortsvektor nach S eingeben. |  |
||
|
 |
Die Vektoren
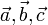 werden als nächstes im
Mat-Menü eingegeben. Anschließend wird im
Run-Menü das Volumen berechnet.
werden als nächstes im
Mat-Menü eingegeben. Anschließend wird im
Run-Menü das Volumen berechnet.| Im Hauptmenü das Mat-Menü auswählen. |  |
| Im Mat-Menü 'Mat A : 3 x 3' auswählen. |  |
Hier nun
die entsprechenden Richtungsvektoren 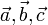 eingeben. Als
nächstes im Run-Menü das Volumen berechnen. eingeben. Als
nächstes im Run-Menü das Volumen berechnen. |
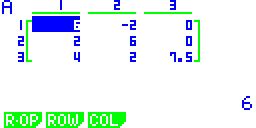 |
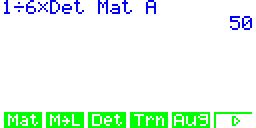
| Folgende
Tastenfolge muss im Run-Menü für die Determinante verwendet werden: 1. OPT-Taste, danach F2 2. F3, danach F1 3. Alpha-Taste, danach A Es ergibt sich ein Volumen von VTetraeder = 50 VE. |
 |
Antwortsatz:
Das Volumen der Pyramide beträgt 50 Volumeneinheiten.
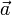 ablesen.
ablesen. 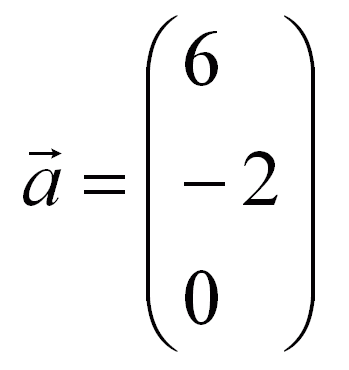
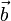 ablesen.
ablesen.
 ablesen.
ablesen.